یکی از دانشجویان سال چهارم کالج، به نقل از خودش، تصمیم گرفت استعداد و افق موسیقی خود را گسترش دهد. این جرقه‌ی ذهنی باعث شد به انجمن موسیقی آغازین بپیوندد. ورودش به کالج از طریق بورس تحصیلی ویولا میسر شد، از این رو، وقتی در آنجا به سر می‌برد در ارکستر مشغول نواختن بود. علاوه بر آن، بر موسیقی مجلسی و قطعات تک‌نوازی ویولا کار می‌کرد. به گفته‌ی خود او:

با اینکه از موسیقی آغازین لذت می‌بردم می‌خواستم نوعی جدید از آن را تجربه کنم. در انجمن، ویولن باروک نواختم و از بسیاری از تکنیک‌های من به‌عنوان یک نوازنده‌ی ویولن مدرن به‌خوبی استقبال شد. آلت موسیقی را برداشتم و اندکی متفاوت‌تر به نشانه‌ی تعظیم سر فرود آوردم، اما در کل می‌توانستم آلت موسیقی را سریع بردارم. خواندن موسیقی هم داستان دیگری بود.

عمده‌ی مردم در کلاس‌های موسیقی با کلید تربل (treble clef) و بیس (bass clef) سروکار دارند. وقتی مادرش به او درس موسیقی آموخت بسیار جوان بود، با این حال هنوز هم آن حس کمال‌طلبی گذشته را به‌یاد می‌آورد؛ وقتی او بر این ایده که مکان یک نقطه در یک آرایه از خطوط و فواصل با کلید ویژه‌ای بر پیانو یا زیروبمی مشخصی متناظر است تسلط یافت. کلید تربل بر G بالای C میانی استوار است. کلید بیس از F پایین C میانی استفاده می‌کند. 

گام بزرگ  A C از وسط کلیدهای بیس (پایینی) و تربل (بالایی) نوشته می‌شود. دوتا نقطه روی کلید بیس به F پایین C میانی و دایره‌های کلید تربل به G بالای C میانی اشاره می‌کند. اعتبار: مارتین مارته سینگر ویکی‌مدیا (CC BY-SA 4.0).

گستره‌ی بسیاری از آلات موسیقی کاملاً در کلید تربل یا بیس جا می‌گیرد. ممکن است در هنگام ضرورت از طریق یک اکتاو تنظیم شود. البته، موسیقی پیانو از هر دو کلید بهره می جوید. اما ویولا اندکی پایین‌تر است تا همیشه از کلید تربل استفاده کند و به همین ترتیب برای به‌کار گرفتن پیوسته کلید بیس اندکی بالاتر قرار می‌گیرد. وقتی او شروع به نواختن ویولا کرد، توانست کلید آلتو را بخواند؛ C میانی دقیقاً وسط حامل قرار گرفته است، در نهایت او به موسیقی‌خوانی معادل یک شخص سه زبانی مبدل شد.

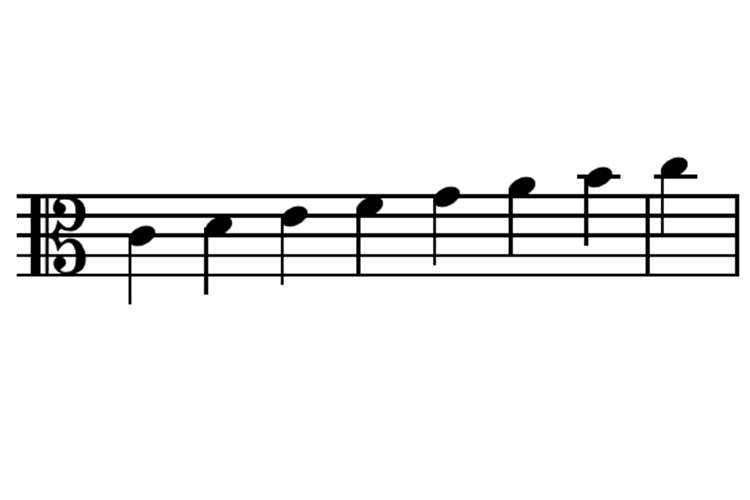گام بزرگ A C در کلید آلتو نوشته می‌شود. با شروع از C میانی. اعتبار: هایسینث ویکی‌مدیا

چندزبانی بودن وی محدودیت‌های خودش را داشت. وی می‌گوید:

من همه‌ی سه کلید را می توانستم بخوانم؛ اما چیزی که می‌خواستم بنوازم موسیقی اصلی نوشته‌شده برای چلو یک اکتاو بالاتر یا موسیقی اصلی نوشته‌شده برای فلوت یا ویولن یک اکتاو پایین‌تر بود، کارهایی که روی پیانو بدیهی جلوه می‌کنند. من برای خواندن کلید بیس بالای یک اکتاو یا کلید تربل پایین یک اکتاو، به ترتیب با کمی سختی و تقلا مواجهه بودم. کلید تنور شبیه کلید آلتواست؛ با این تفاوت C آن یک خط بالاتر قرار می‌گیرد و همین موضوع مرا تماماً سردرگم می‌کرد. آنگونه که خودم انتظار داشتم فصیح و روان نبودم.

انجمن موسیقی آغازین محدودیت‌های وی را برانگیخت. موسیقی از عصر باروک و قبل از آن با اعداد کوچکی از کلیدهایی که ما اکنون به‌کار می‌گیریم، نماد‌گذاری نمی‌شد. او می‌توانست موسیقی را در کلید ویولن فرانسوی (این شبیه کلید تربل است اما G در خط پایینی قرار دارد به‌جای آنکه بالای آن قرار گیرد)،‌ کلید سپرانو (کلید C شبیه کلید آلتو و تنور است و C روی خط پایینی قرار دارد) و کلیدهای غیرمعمول کنونی بخواند. این موضوع برایش تأثیرگذار بود. نام‌های نت زیادی در موسیقی خود باید نوشتت و با این حال در تمرین مرتکب اشتباهات زیادی می‌شد.

ترمی که با انجمن موسیقی آغازین شروع به نواختن کرد، کلاس جبر مجرّد برداشت. جبر مجرد به ساختارهای مجموعه‌ای از اعداد و تقارن‌ها می‌پردازد. برخی اوقات مردم را به ارتباطات بسیار متفاوت بین اشیا ریاضیاتی و تبدیلات تشویق می‌کند و روابط بین اشیا را به‌عنوان پایه‌ای نشان میدهد که برای ادراک آن اشیا لازم است.

این ترم، همچون جرقه‌ای برای ذهن وی بود. از طرفی، تقلا و دشواری‌های کلید موسیقیایی آغازین کمابیش برایش قابل حل شدند. وی طی پیشرفتی که برایش به وقوع پیوست می‌گوید:

در آغاز یک قطعه، به کلید نگاه می‌کردم تا مسیر خود را دریابم و بعد از آن بقیه نت‌ها رابطه بین یک پیچ و پیچ بعدی خود را به راحتی نشان می دادند. من فواصل را می‌خواندم نه زیروبمی‌ها را. من فوق‌العاده و کامل نبودم اما حس می‌کردم در یک شب قفل مرحله موسیقی‌خوانی جدیدی را باز کرده‌ام.

او از احساسی می‌گوید که سفرش به جبر مجرد و فصاحتش در کلید جدید را به هم مرتبط می‌کرد. او برای گذاشتن این ارتباط در قالب کلمات تقلای بسیاری کرد. جنبه‌های ارتباطی و ساختاری جبر مجرد او را قادر به دیدن کلیدها کرد؛ کلیدها به‌عنوان روابط بین نت‌ها بیشتر از صرف زیروبمی‌های مطلق. او از پرداختن به قضیه‌ی ویژه‌ یا بینشی در جبر مجرد اجتناب می‌کرد؛ به‌نحوی که صریحاُ قابل اطلاق باشد.

در سال قبل، قضیه‌ی مهمی در ریاضیات به نام یوندا لما در باب نظریه دسته‌ها فراگرفت (بنا به گفته امیلی ریل مهمان My Favorite Theorem، این قضیه موردعلاقه هرنظریه‌پرداز دسته‌ای است). با اینکه او نظریه‌پرداز دسته‌ای نیست؛ اما شرح تای-دانائه برادلی از یوندا لما را مفید تلقی می‌کرد، به‌ویژه ایده‌ی بزرگی که او در این پست درباره چشم‌انداز یوندا به اشتراک گذاشته است. او می‌نویسد لب مطلب یوندا لما یا حداقل دو مورد از استدلال‌های آن این است: اشیا ریاضی روابط آن‌ها تماماً با دیگر اشیا تعیین می‌شود.

مدتی طول کشید تا وی این ارتباط را به صورت صریحی دریابد، اما تصور می‌کرد چشم‌انداز یوندا تغییر ذهنی‌ای را توصیف می‌کند که وی در انجمن موسیقی آغازین به آن دچار شده است. متن دقیق نت‌ها در خواندن موسیقی نوشته‌شده در کلیدهای مبهم و ناشناس نیست که مهم است، بلکه ارتباط بین آن‌ها مورد توجه است. از وقتی این تغییر در دیدگاه وی ظاهر شد، ترانسپوز (ترانهش) موسیقی به کلیدهای مختلف برایش وجه ساده‌تری پیدا کرد و خواندن کلید تربل و بیس در هر اکتاوی که نیتش می‌کرد کار دشواری نبود.

برخی نوازندگان ارگ و پیانو می توانند بدون هیچ تقلایی موسیقی را ترانهش کنند تا بتوانند نیازهای دسته کر کلیسا یا اجراکننده‌های تئاتر موسیقی را برطرف کنند. به تصور او، آن‌ها قبلاً به چشم‌انداز یوندا دست بافته‌اند، حتی اگر این چیزی نباشد که خودشان بدان اقرار کنند. آن‌ها الزاماً از طریق کلاس‌های پیشرفته‌ی ریاضی به این موضع نرسیده‌اند؛ اما از نظر وی کلاس جبر مجرد جرقه‌ای بود که به آن نیاز داشت تا به دور از هر یک از مجموعه‌ی این زیروبمی، بر روابط بین آن‌ها متمرکز شود. وی الهام موسیقیایی خود را از ریاضی بدین نحو توصیف می کند:

ادعا نمی‌کنم مطالعه‌ی جبر مجرد یا نظریه‌ی دسته‌ای مهارت‌های موسیقی‌خوانی شما را بهبود می‌بخشد؛ ساخت موسیقی بدون مطالعه‌ی کتاب ریاضی معمولاً بهترین راه پیشرفت در موسیقی است؛ اما تفکر روی این روابط تجربه مرا هم در حوزه ریاضی و هم موسیقی غنی کرد و امیدوارم همین نتیجه زا برای شما داشته باشد.